Новая математическая формула способна изменить здравоохранение, энергетику и пищепром всего мира

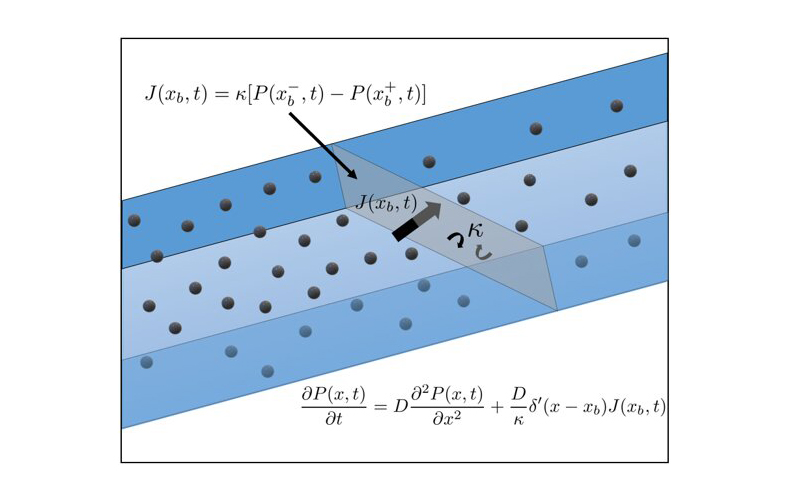
Уравнение диффузии является основным инструментом для изучения динамики движения свободной броуновской частицы, но при наличии пространственных неоднородностей в виде проницаемого материала фундаментальное уравнение не работает.

Случайное движение повсеместно, оно проявляется во многих физических, биологических и социальных системах и традиционно моделируется как диффузия в однородной среде. Но в реальных системах однородность окружающей среды часто перемежается пространственными неоднородностями, которые существенно мешают диффузионному переносу. Во многих случаях эти неоднородности обусловлены наличием проницаемых границ раздела, часто называемых полупроницаемыми или частично проницаемыми барьерами. Они появляются в микроскопических масштабах в различных пористых средах, таких как биологические ткани, а также в более крупных масштабах, когда целые организмы взаимодействуют с химическими или физическими объектами.

Ранее попытки математиков представить движение в среде с проницаемыми барьерами, например, в пористых материалах — губках, биологических тканях, полимерах — были ограниченными и не точными. Новое уравнение, выведенное учеными из Бристольского университета, показывает, что диффузионное движение через проницаемый материал может быть точно смоделировано. Можно даже говорить о значительном прогрессе в представлении движения для широкого спектра объектов — от микроскопических частиц и природных организмов до искусственно созданных устройств. Ведь животные, клеточные организмы и люди регулярно сталкиваются с проницаемыми барьерами.

Чтобы вывести новое уравнение, ученым пришлось представить случайное движение микроскопическим способом, а затем они уменьшили масштаб, чтобы описать процесс макроскопически. Исследователи рассматривали несмещенный случайный блуждающий объект с ближайшим соседом на бесконечной одномерной решетке. Они использовали популярную модель случайного блуждания, а также уравнение Фоккера-Планка и соответствующее обратное уравнение Колмогорова — последние были задействованы для исследования статистики первого прохождения и локального времени. Так и удалось вывести новое уравнение. Результаты работы появились в журнале Physical Review Research.

По мнению авторов, необходимы дальнейшие исследования, чтобы начать применять новый математический инструмент на практике. Например, возможность точного смоделировать диффузию молекул воды через биологическую ткань улучшит интерпретацию показаний МРТ. Также ученые смогут более точно представлять, как воздух проникает сквозь упаковочные материалы для пищевых продуктов — это поможет точнее определить срок годности продуктов и риск их загрязнения. А количественная оценка поведения животных, добывающих пищу и взаимодействующих с макроскопическими барьерами, такими как заборы и дороги, в конечном итоге поможет более точно прогнозировать последствия изменения климата.